Menghitung Ketidakpastian Pengukuran dalam Fisika
Wednesday 15 January 2020
Add Comment
Ketidakpastian Pengukuran dalam Fisika terkait
dengan hasil pengukuran, yang mencirikan dispersi dari nilai-nilai yang
cukup dapat dikaitkan dengan ukur. ketidakpastian umumnya mencakup
banyak komponen yang dapat dievaluasi dari standar deviasi eksperimen
berdasarkan pengamatan berulang.
Di bawah ini merupakan ulasan tentang ketidakpastian pengukuran dalam fisika semoga bermanfaat!
Ketidakpastian Pengukuran dalam Fisika
Setiap pengukuran tidak pernah tetap dan
mempunyai taksiran nilai. Mengukur adalah membandingkan suatu besaran
yang dimiliki suatu alat yang besarannya sejenis dengan cara membaca
skala.
Tujuan pengukuran adalah menentukan nilai
besaran ukur. Hasil pengukuran merupakan nilai taksiran besaran ukur.
Karena hanya merupakan taksiran maka setiap hasil pengukuran mempunyai
kesalahan.
Konsep ketidakpastian (uncertainty)
merupakan bagian penting dari hasil suatu analisis kuantitatif. Tanpa
pengetahuan tentang ketidakpastian pengukuran, maka pernyataan suatu
hasil pengujian belum dapat dikatakan lengkap. Walaupun konsep
ketidakpastian pengukuran telah lama dikenal oleh para ilmuwan, namun
petunjuk formal untuk evaluasi ketidakpastian baru diterbitkan pada
tahun 1993.
Petunjuk tersebut adalah “Guide to the Expression of Uncertainty in Measurement” yang diterbitkan oleh ISO melalui kolaborasi dengan BIPM (Bureau International des Poids et Measures ; International Bureau of Weights and Measures), IUPAC (International Union of Pure and Applied Chemistry), IUPAP (International Union of Pure and Applied Physics), dan OIML (Organisation Internationale de Metrologie Legale, International Organization of Legal Metrology). Dokumen ini dikenal dengan ISO-GUM dan berlaku untuk semua area pengujian secara luas.
Ketidakpastian memiliki beberapa arti yaitu
“ragu-ragu”, “kekurangpercayaan” dan “derajat ketidakyakinan”. Namun,
ketidakpastian secara metrologis telah didefinisikan oleh ISO (atau VIM,
Vocabulaire International de Metrologie) sebagai berikut :
“non-negative
parameter characterizing the dispersion of quantity values being
attributed to a measurand, based on the information used”.
Jadi ketidakpastian merupakan suatu parameter non-negative yang menggambarkan sebaran nilai kuantitatif suatu hasil pengukuran (measurand), berdasarkan informasi yang digunakan.
Namun bahasan tentang konsep ketidakpastian
tidaklah utuh tanpa membahas juga tentang konsep traceability
(ketertelusuran). Menurut ISO istilah traceability secara metrologis
didefinisikan sebagai berikut :
“property of a
measurement results whereby the result can be related to a reference
through a documented unbroken chain of calibrations each contributing to
the measurement uncertainty”
Jadi ketertelusuran merupakan sifat dari
pengukuran/pengujian, dimana hasil tersebut dapat dihubungkan ke suatu
nilai acuan melalui mata rantai kalibrasi yang tidak terputus yang
terdokumentasi, dimana masing-masing mata rantai berkontribusi terhadap
ketidakpastian pengukuran/pengujian. Dapat dicermati bahwa definisi
ini secara tegas menggambarkan keterkaitan antara ketidakpastian dengan
ketertelusuran.
Jika ketertelusuran menyatakan keterkaitan
hasil terhadap nilai benar berdasarkan suatu acuan, sementara
ketidakpastian menggambarkan sebaran nilai kuantitatif dari hasil uji,
maka tidaklahkeliru pandangan yang menyatakan bahwa ketidakpastian
merupakan suatu rentang dimana nilai benar itu berada, sebagaimana
diilustrasikan pada Gambar 1.
Gambar 1. Ilustrasi konsep ketidakpastian yang digambarkan merupakan suatu rentang (± U), dan mencakup nilai benar (X)
Jadi kita tidak dapat mengevaluasi nilai
ketidakpastian suatu hasil pengukuran/pengujian sebelum aspek
ketertelusuran dari pengukuran/pengujian tersebut secara jelas
dinyatakan.
denganx adalah nilai pendekatan terhadap nilai benar x0 dan Δx
adalah ketidakpastiannya.
Misalkan seorang pengamat mengukur panjang pensil menggunakan mistar diperoleh nilai benar sebesar 12 cm. Skala terkecil dari mistar adalah 1 mm atau 0,1 cm makaΔx=12×nst=12×0,1
. Hasil pengukuran tunggal ini dituliskan sebagaiL=12±0,05 cm.
x0
adalah nilai rata – rata dari data yang diperoleh (x¯ ). Sedangkan untuk nilai ketidakpastiannya (Δx ) dapat digantikan oleh nilai simpangan baku nilai rata-rata sampel. Secara matematis dapat ditulis sebagai berikut.
x¯=x1+x2+x3+…..+xnN=∑xiN
Δx=1NN∑x2i−(∑xi)2N−1−−−−−−−−−−−√
Keterangan:
x¯
: hasil pengukuran yang mendekati nilai benar
Δx
: ketidakpastian pengukuran
N
: banyaknya pengukuran yang dilakukan.
Ketidakpastian menunjukkan seberapa dekat hasil pengukuran mendekati nilai sebenarnya. Semakin kecil nilainya maka semakin dekat hasil pengukuran dengan nilai sebenarnya. Pada pengukuran tunggal ketidak pastianΔx
disebut ketidakpastian mutlak.
Pada pengukuran berulang dikenal istilah ketidak pastian relatif, yaitu perbandingan ketidakpastian pengukuran berulang dengan nilai rata-rata pengukuran.
ketidakpastian relatif =Δxx¯×100
Nilai ketidakpastian relatif menentukan banyaknya angka yang boleh disertakan pada laporan hasil pengukuran. Aturan banyaknya angka yang dapat dilaporkan dalam pengukuran berulang adalah sebagai berikut.
x=x0±12 nst=1,80±0,005 mm
Δx=1NN∑x2i−(∑xi)2N−1−−−−−−−−−−−√=165243,16−5241,765−−−−−−−−−−√=0,08 cm
ketidakpastian relatif=0,0812,1×100%=0,7%.
Karena ketidak pastian relatif dekat dengan 1% maka pelaporan hasil pengukuran hanya berhak dengan 3 angka. Jadi penulisan hasil pengukurrannya adalahx=12,1±0,08
dan(25,0±0,05) cm. Nilai prosentase ketidak pastian volume silinder tersebut adalah….
Penyelesaian:
Volume silinder adalahV=14πd2t , sehingga prosentase ketidakpastiannya adalah
%ΔV
%ΔV=2%Δd+%Δt=2×0,0580,0×100%+0,0525,0×100%=0,125%+0,2%=0,325%.
Penelusuran yang terkait dengan Menghitung Ketidakpastian Pengukuran
dengan
adalah ketidakpastiannya.
Jenis Ketidakpastian
Ada dua jenis ketidakpastian pengukuran, yaitu pengukuran tunggal dan pengukuran berulang.1. Ketidakpastian pengukuran tungal
Pengukuran tunggal merupakan pengukuran yang hanya dilakukan satu kali. Pada pengukuran tunggal, nilai yang dijadikan pengganti nilai benar adalah hasil pengukuran itu sendiri dan ketidakpastiannya diperoleh dari setengah nilai skala terkecil (nst) instrumen yang digunakan.Misalkan seorang pengamat mengukur panjang pensil menggunakan mistar diperoleh nilai benar sebesar 12 cm. Skala terkecil dari mistar adalah 1 mm atau 0,1 cm maka
. Hasil pengukuran tunggal ini dituliskan sebagai
2. Ketidakpastain pengukuran berulang
Agar mendapatkan hasil pengukuran yang akurat, harus dilakukan pengukuran secara berulang. Pada pengukuran berulang nilai terbaik untuk menggantikan nilai benaradalah nilai rata – rata dari data yang diperoleh (
Keterangan:
: hasil pengukuran yang mendekati nilai benar
: ketidakpastian pengukuran
: banyaknya pengukuran yang dilakukan.
Ketidakpastian menunjukkan seberapa dekat hasil pengukuran mendekati nilai sebenarnya. Semakin kecil nilainya maka semakin dekat hasil pengukuran dengan nilai sebenarnya. Pada pengukuran tunggal ketidak pastian
disebut ketidakpastian mutlak.
Pada pengukuran berulang dikenal istilah ketidak pastian relatif, yaitu perbandingan ketidakpastian pengukuran berulang dengan nilai rata-rata pengukuran.
Nilai ketidakpastian relatif menentukan banyaknya angka yang boleh disertakan pada laporan hasil pengukuran. Aturan banyaknya angka yang dapat dilaporkan dalam pengukuran berulang adalah sebagai berikut.
- relatif 10 % berhak atas dua angka
- relatif 1%berhak atas tiga angka
- relatif 0,1% berhak atas empat angka
Contoh Soal & Pembahasan Ketidakpastian
- Pak Arifin mengukur ketebalan uang logam menggunakan mikrometer
sekrup dan diperoleh hasil bahwa ketebalan uang logam adalah 1,80 mm.
Penulisan hasil pengukuran yang tepat adalah…
.Penyelesaian:
x0=1,80
- Suatu pengukuran berulang terhadap panjang pensil diperoleh hasil seperti berikut.
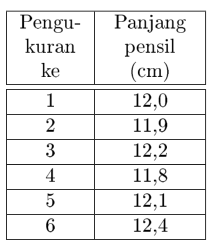
Laporkan hasil pengukuran berulang tersebut lengkap dengan ketidakpastiannya!
Penyelesaian:
Untuk mempermudah perhitung dapat digunakan tabel seperti berikut.
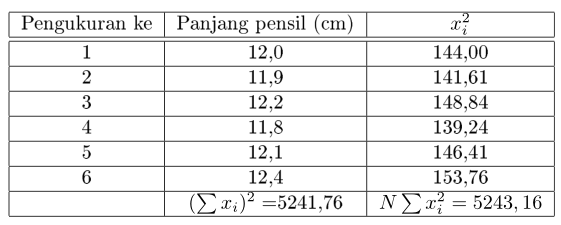
x¯=x1+x2+x3+…..+xnN=∑xiN=72.46=12,1
Karena ketidak pastian relatif dekat dengan 1% maka pelaporan hasil pengukuran hanya berhak dengan 3 angka. Jadi penulisan hasil pengukurrannya adalah
- cm.
- Pengukuran diameter dan tinggi sebuah silinder adalah
(80,0±0,05)
dan
Penyelesaian:
Volume silinder adalah
Penelusuran yang terkait dengan Menghitung Ketidakpastian Pengukuran
- bagaimana menentukan ketidakpastian (ralat) pengukuran
- pengertian pengukuran dan ketidakpastian dalam pengukuran
- ketidakpastian pengukuran pdf
- soal dan jawaban pengukuran berulang
- berikan contoh soal pengukuran berulang
- dasar pengukuran dan ketidakpastian ebook
- laporan pengukuran berulang
- pengertian teori ketidakpastian fisika dasar



0 Response to "Menghitung Ketidakpastian Pengukuran dalam Fisika"
Post a Comment