Pembahasan Hukum Keppler tentang Gerak Planet Lengkap

Kampungilmu.web.id - Hukum keppler membahas tentang gerak planet ketika melakukan revolusi, yaitu gerakan planet mengelilingi matahari. Hukum Keppler di dasari oleh pengamatan yang dilakukan Ticho Brahe . Ticho Brahe melakukan penelitian untuk mengamati gerak-gerak planet selama bergerak mengelilingi matahari di ruang angkasa. Keppler merupakan seorang matematikawan yang paling termasyur di jamannya. Pendapat Keppler tantang gerak planet mendukung teori heliosentris yang dikemukakan oleh Copernicus. Pendapat Keppler tersebut dikenal dengan hukum Keppler.

gambar 1

Menurut Keppler lintasan planet mengelilingi matahari tidak berbentuk lingkaran sempurna, melainkan berbentuk elips. Pernyataan tersebut dikenal sebagai hukum I keppler. Bunyi hukum I Keppler “ lintasan yang ditempuh oleh sebuah planet ketika bergerak mengelilingi matahari berbentuk elips, dan matahari terletak sebagai titik fokus atau pusatnya”. Untuk lebih memahami hukum I Keppler, perhatikan gambar 1. 

Dari bunyi hukum I Keppler dapat ditarik suatu kesimpulan bahwa :
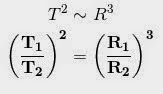
a. jarak antara planet dan matahari tidak tetap. Jarak terpendek antara planet dan matahari disebut perihelium, sedangkan jarak terjauh antara planet dan matahari disebut aphelium.
b.  matahari berperan sebagai penyeimbang dari semua orbit planet di tatasurya.

Jika hukum I Keppler menjelaskan tentang orbit planet, hukum II Keppler menjelaskan tentang kecepatan planet ketika mengorbit matahari. Bunyi hukum II Keppler “ sebuah planet akan menyapu luasan yang sama dalam selang waktu yang sama ketika bergerak mengelilingi matahari”. Untuk lebih memahami hukum  II Keppler perhatikan gambar 1. Luas yang ditempuh ketika planet bergerak dari A ke B akan sama dengan luas yang ditempuh ketika planet bergerak dari C ke D. Waktu yang diperlukan oleh planet untuk bergerak dari A ke B akan sama dengan waku yang diperlukan untuk bergerak dari C ke D. ketika planet berada dekat dengan matahari (perihelium) planet bergerak cepat dan ketika planet berada jauh dari matahari planet bergerak lebih lambat (aphelium).

Hukum III Keppler menjelaskan tentang hubungan antara jarak planet dari matahari dengan periode planet mengelilingi matahari. Hukum III Keppler berbunyi “kuadrat periode sebuah planet mengelilingi matahari akan berbanding lurus dengan pangkat tiga jarak rata-rata planet dari matahari”

Hukum III Keppler dirumuskan :

Dimana :
T1 = periode planet 1
T2 = periode planet 2
R1= jarak rata-rata planet 1 dari matahari
R2 = jarak rata-rata planet 2 dari matahari

Pengenalan Tiga Hukum Kepler

Secara Umum

Hukum hukum ini menjabarkan gerakan dua badan yang mengorbit satu sama lainnya. Massa dari kedua badan ini bisa hampir sama, sebagai contoh Charon—Pluto (~1:10), proporsi yang kecil, sebagai contoh. Bulan—Bumi(~1:100), atau perbandingan proporsi yang besar, sebagai contoh Merkurius—Matahari (~1:10,000,000).

Dalam semua contoh di atas, kedua badan mengorbit mengelilingi satu pusat massa, barycenter, tidak satu pun berdiri secara sepenuhnya di atas fokus elips. Namun, kedua orbit itu adalah elips dengan satu titik fokus di barycenter. Jika rasio massanya besar, sebagai contoh planet mengelilingi Matahari, barycenternya terletak jauh di tengah obyek yang besar, dekat di titik massanya. Di dalam contoh ini, perlu digunakan instrumen presisi canggih untuk mendeteksi pemisahan barycenter dari titik masa benda yang lebih besar. Jadi, hukum Kepler pertama secara akurat menjabarkan orbit sebuah planet mengelilingi Matahari.

Karena Kepler menulis hukumnya untuk aplikasi orbit planet dan Matahari, dan tidak mengenal generalitas hukumnya, artikel ini hanya akan mendiskusikan hukum di atas sehubungan dengan Matahari dan planet-planetnya.

Hukum Pertama

Figure 2: Hukum Kepler pertama menempatkan Matahari di satu titik fokus edaran elips.

"Setiap planet bergerak dengan lintasan elips, Matahari berada di salah satu fokusnya."

Pada zaman Kepler, klaim di atas adalah radikal. Kepercayaan yang berlaku (terutama yang berbasis teori epicycle) adalah bahwa orbit harus didasari lingkaran sempurna. Pengamatan ini sangat penting pada saat itu karena mendukung pandangan alam semesta menurut Kopernikus. Ini tidak berarti ia kehilangan relevansi dalam konteks yang lebih modern.

Meski secara teknis elips yang tidak sama dengan lingkaran, tetapi sebagian besar planet planet mengikuti orbit yang bereksentrisitas rendah, jadi secara kasar bisa dibilang mengaproksimasi lingkaran. Jadi, kalau ditilik dari pengamatan jalan edaran planet, tidak jelas kalau orbit sebuah planet adalah elips. Namun, dari bukti perhitungan Kepler, orbit-orbit itu adalah elips, yang juga memeperbolehkan benda-benda angkasa yang jauh dari Matahari untuk memiliki orbit elips. Benda-benda angkasa ini tentunya sudah banyak dicatat oleh ahli astronomi, seperti komet dan asteroid. Sebagai contoh, Pluto, yang diamati pada akhir tahun 1930, terutama terlambat diketemukan karena bentuk orbitnya yang sangat elips dan kecil ukurannya.

Hukum Kedua

Figure 3: Illustrasi hukum Kepler kedua. Bahwa Planet bergerak lebih cepat di dekat Matahari dan lambat di jarak yang jauh. Sehingga, jumlah area adalah sama pada jangka waktu tertentu.

"Luas daerah yang disapu pada selang waktu yang sama akan selalu sama."

Secara matematis:

dimana adalah "areal velocity".

Hukum Ketiga

Planet yang terletak jauh dari Matahari memiliki perioda orbit yang lebih panjang dari planet yang dekat letaknya. Hukum Kepler ketiga menjabarkan hal tersebut secara kuantitatif.

"Perioda kuadrat suatu planet berbanding dengan pangkat tiga jarak rata-ratanya dari Matahari."

Secara matematis:

dengan adalah perioda orbit planet dan adalah sumbu semimajor orbitnya.

Konstant proporsionalitasnya adalah semua sama untuk planet yang mengedar Matahari.

 

Sejarah

Pada tahun 1601 Kepler berusaha mencocokkan berbagai bentuk kurva geometri pada data-data posisi Planet Mars yang dikumpulkan oleh Tycho Brahe. Hingga tahun 1606, setelah hampir setahun menghabiskan waktunya hanya untuk mencari penyelesaian perbedaan sebesar 8 menit busur (mungkin bagi kebanyakan orang hal ini akan diabaikan), Kepler mendapatkan orbit planet Mars. Menurut Kepler, lintasan berbentuk elips adalah gerakan yang paling sesuai untuk orbit planet yang mengitari matahari. Pada tahun 1609, dia mempublikasikan Astronomia Nova yang menyatakan dua hukum gerak planet. Hukum ketiga tertulis dalam Harmonices Mundi yang dipublikasikan sepuluh tahun kemudian.

Share this post