Lengkap Persamaan Linear Satu Variabel dan Dua Variabel dan Penyelesaiannya

Persamaan Linear Satu Variabel

Temen-temen perhatikan beberapa persamaan berikut :

3x+5 = 7
2-3y = 6
z+3 = 4z

Jika kita lihat dari persamaan diatas, variabel dari persamaan satu adalah x, pada persamaan dua adalah y dan pada persamaan tiga adalah z. Persamaan-persamaan tadi merupakan contoh bentuk dari persamaan linear satu variabel, karena masing-masing persamaan memiliki satu variabel dan berpangkat satu. Variabel x, y, z merupakan variabel pada himpunan tertentu yang ditentukan pada masing-masing persamaan tersebut.

Persamaan linear satu variabel dapat dinyatakan dalam bentuk ax = b atau ax + b = c dimana a, b dan c adalah konstanta, dengan a ≠ 0 dan x merupakan variabel pada suatu himpunan.

Perhatikan contoh soal berikut.

Tentukan himpunan penyelesaian persamaan berikut.

3x+1 = 4; x∈B ( B bilangan bulat )
2y+5 = -3y+7; y∈Q ( Q bilangan rasional )

Penyelesaian :

1. 3x+1 = 4

⇔3x+1-1= 4-1

⇔ 3x = 3

⇔ 1/3. 3x = 3. 1/3

⇔ x = 1

Sehingga himpunan penyelesaiannya adalah { 1 }.

2. 2y+5 = -3y+7

⇔2y+5-5 = -3y+7-5

⇔ 2y = -3y+2

⇔ 2y+3y =2

⇔ 5y =2

⇔ 1/5.5y = 1/5.2

⇔ y = 2/5

sehingga himpunan penyelesaiannya adalah {2/5}.

Persamaan Linear Dua Variabel

Jika kita ingat bahwa persamaan garis lurus pada bidang cartesius dapat dinyatakan dalam bentuk ax + by = c dimana a, b, c merupakan konstanta real dengan a, b ≠ 0 serta x, y merupakan variabel pada himpunan bilangan real.

Perhatikan persamaan-persamaan berikut ini.

a. x + 6 = y

b. 2a – b = 5

c. 3p + 6q = 4

Persamaan-persamaan diatas merupakan contoh bentuk persamaan linear dua variabel. Varibel untuk persamaan x+6 =y adalah x dan y, variabel pada persamaan 2a-b = 5 adalah a dan b, sedangkan variabel pada persamaan 3p+6q =4 adalah p dan q.

Jika kita perhatikan pada contoh persamaan diatas, banyaknya variabel ada dua dan masing-masing berpangkat satu.

Persamaan linear dua variabel dapat dinyatakan dalam bentuk ax+by = c dengan a, b, c ∈ R, a, b ≠ 0, dan x, y suatu variabel.

Nah ketika kita menemukan persamaan dua variabel seperti ini lalu bagaimana cara kita menyelesaikan untuk mendapatkan himpunan penyelesaiannya. kita bahas yuu

Persamaan x+y = 5 masih merupakan kalimat terbuka, yang artinya belum mempunyai nilai kebenaran. Jika kita ganti nilai x dengan 1 maka nilai y yang memenuhi adalah 4. Karena pasangan bilangan (1,4) memenuhi persaamaan tersebut, maka persamaan x+y = 5 menjadi kalimat yang benar. Sehingga dapat dikatakan bahwa (1,4) merupakan salah satu penyelesaian dari persamaan x+y = 5. Dan apakah hanya (1,4) saja yang merupakan penyelesaian persamaan tersebut? Untuk menentukan himpunan penyelesaian dari x+y = 5 dimana x dan y adalah variabel pada bilangan cacah maka kita harus mencari x dan y yang memenuhi persamaan tersebut. Agar lebih mudah kita dapat membuat tabel seperti berikut.

selanjutnya jika gambarkan pada bidang cartesius akan tampak seperti gambar berikut.

Apabila x dan y variabel pada bilangan cacah berupa noktah / titik, tetapi jika x dan y variabel pada himpunan bilangan real maka titik-titik tersebut dihubungkan sehingga membentuk garis lurus. Perhatikan gambar berikut.

Menyelesaikan Persamaan Linear Satu Variabel (PLSV)

Persamaan adalah suatu pernyataan matematika dalam bentuk simbol yang menyatakan bahwa dua hal adalah persis sama. Dari bentuk-bentuk 3(x – 1) + x dan –x + 7, kita dapat membentuk persamaan

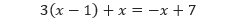
yang merupakan suatu persamaan linear satu variabel (PLSV). Untuk menyelesaikan suatu persamaan, kita harus menentukan nilai dari x sedemikian sehingga persamaan tersebut menjadi benar, yang berarti, nilai dari ruas kiri sama dengan ruas kanan. Perhatikan tabel berikut.

Berdasarkan tabel di atas, kita dapat menemukan bahwa persamaan 3(x – 1) + x = –x + 7 akan bernilai benar ketika kita mengganti x dengan bilangan 2, dan akan salah jika kita mengganti x dengan bilangan selain

2. Bilangan pengganti yang dapat menyebabkan suatu persamaan bernilai benar disebut selesaian atau akar.

Menyelesaikan persamaan dengan menggunakan tabel akan memakan waktu yang cukup lama. Untuk itu, kita dapat menuliskan suatu persamaan yang diberikan ke dalam persamaan ekuivalen yang lebih sederhana, sampai kita mendapatkan solusi yang diminta. Persamaan-persamaan yang ekuivalen adalah persamaan-persamaan yang memiliki himpunan selesaian sama, dan diperoleh dari penyederhanaan kedua ruas persamaan dengan menggunakan sifat-sifat penjumlahan, perkalian, dan distributif dari suatu persamaan, sampai diperoleh suatu persamaan dalam bentuk x = konstanta.

Sifat Penjumlahan dan Perkalian Suatu Persamaan
Jika A, B, dan C merupakan bentuk-bentuk aljabar dan A = B, maka A + C = B + C, AC = BC, dan A/C = B/C (C ≠ 0).

Dengan kata lain, berdasarkan sifat penjumlahan suatu persamaan, kita dapat menambahkan suatu bilangan atau bentuk aljabar lain ke dalam ruas kanan dan kiri persamaan tersebut. Pernyataan yang serupa dapat dibuat untuk menyatakan sifat perkalian suatu persamaan. Sifat-sifat dari persamaan ini dapat dikombinasikan untuk dijadikan panduan dalam menyelesaikan suatu persamaan linear. Sebagai catatan, tidak semua langkah dalam panduan ini diperlukan dalam menyelesaikan setiap persamaan.

Berikut ini merupakan panduan/langkah-langkah dalam menyelesaikan persamaan linear satu variabel.

Hilangkan tanda kurung dengan menggunakan sifat distributif, kemudian operasikan suku-suku yang serupa.
Gunakan sifat penjumlahan suatu persamaan untuk menulis persamaan tersebut sehingga semua variabel berada di satu ruas, sedangkan semua konstanta berada di ruas lainnya. Sederhanakan masing-masing ruas.
Gunakan sifat perkalian suatu persamaan untuk menghasilkan persamaan yang berbentuk x = konstanta.
Untuk soal penerapan, jawablah ke dalam kalimat sempurna dan gunakan satuan yang sesuai dengan perintah.

Sebagai contoh pertama, kita akan mencoba menyelesaikan persamaan 3(x – 1) + x = –x + 7 yang merupakan masalah di awal pembahasan ini.

Contoh 1: Menyelesaikan PLSV dengan Menggunakan Sifat-sifat Persamaan

Selesaikan persamaan 3(x – 1) + x = –x + 7.

Pembahasan

Seperti selesaian dengan menggunakan tabel, kita juga memperoleh bahwa selesaian dari persamaan tersebut adalah x = 2.

Untuk menguji selesaian yang kita peroleh, kita dapat mensubstitusikan selesaian ini ke dalam persamaan semula (proses ini sering disebut substitusi-balik), dan pastikan bahwa nilai pada ruas kiri sama dengan ruas kanan. Dari contoh 1 kita mendapatkan:

Jika ada koefisien-koefisien dalam suatu persamaan berbentuk pecahan, kalikan kedua ruas dengan KPK (Kelipatan Persekutuan Terkecil) dari penyebut-penyebutnya, untuk menghilangkan pecahan tersebut. Karena setiap bilangan desimal dapat ditulis ke dalam bentuk pecahan, maka dalam menyelesaikan persamaan yang memuat koefisien desimal, kita dapat mengubah bentuk desimal tersebut ke dalam bentuk pecahan terlebih dahulu.

Contoh 2: Menyelesaikan PLSV dengan Koefisien Pecahan

Tentukan selesaian dari persamaan: 1/4(n + 8) – 2 = 1/2(n – 6).

Pembahasan